Fast and High Efficiency HPLC Separations Using Superficially Porous Particles

In our last blog, we noted that chromatographers often wish that their HPLC separations were faster or that their peaks were better resolved.  We discussed how using columns packed with sub-2 µm fully porous particles (FPPs) can help to achieve both of those goals, but that there’s a price to pay in the form of high instrument operating pressures.  If we don’t have a UHPLC instrument or if we’re concerned about degraded column performance at ultrahigh pressures over the long-term, this might not be our ideal solution.  Fortunately, there’s another option.  Columns packed with 2.7 µm superficially porous particles (SPPs) can provide similar speeds and efficiencies as 1.8 µm fully porous particles but require only a fraction of the operating pressures.  Let’s take a closer look to understand how this is possible.

FPPs and SPPs

To get started, we need to understand the respective

Figure 1 – Dimensions of a 2.7 µm superficially porous particle composed of a 1.7 µm solid silica core and a 0.5 µm-thick porous silica shell

morphologies of fully porous particles (FPPs) and superficially porous particles (SPPs).  In large part, the FPPs used in HPLC columns are spherical silica particles that feature an interconnected network of random pores extending from the particle surfaces all the way to their centers.  So what’s the purpose of all these pores?  They provide nearly all the surface area which is functionalized with stationary phase ligands.  As you might recall, during the course of an HPLC separation, the different analytes will interact with these ligands for different amounts of time, which ultimately leads to peaks being resolved from one another.  If there’s not enough surface area, there will be no separation.

SPPs are similar to FPPs in the sense that they are also spherical silica particles.  But rather than being fully porous, only the outer fraction of the total particle radius features the network of interconnected small pores.  The central portion of the particle is a nonporous, solid silica core.  But doesn’t this reduce the surface area of the stationary phase to the detriment of peak resolution?  It certainly does reduce surface area, but not to the extent that we might at first think.  Consider a 2.7 µm SPP composed of a 1.7 µm nonporous core and a 0.5 µm-thick porous outer shell, like that shown in Figure 1.  Depending on the average pore size, such particles retain 50-75% the surface areas of comparable fully porous particles.  This results in a bit less retention, but the potential benefits can largely outweigh this concern.  To understand these benefits, it will help to consider the kinetic performance curves of FPPs and SPPs.

Kinetic Performance

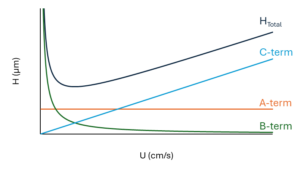
Figure 2 – Typical performance curve (H vs U) with independent contributions from the A-, B-, and C-terms.

For our discussion, let’s think “kinetic performance” to mean plate height (H) versus mobile phase linear velocity (U).  If we plot these variables, the curves for most modern HPLC columns will have the same general shape as that shown by the dark blue trace in Figure 2.  We can see that at very low linear velocities, plate heights will be high.  As we move to faster velocities, plate heights will decrease until we reach an “optimum linear velocity.”  This is the point at which a column exhibits its maximum efficiency.  If we continue to run at faster linear velocities, plate heights will increase again.

The characteristic shape of these H vs U curves is the result of a great many phenomena related to flow and diffusion that work to broaden peaks inside an HPLC column.  To simplify all of these terms, it is convenient to group these phenomena according to their dependence on the mobile phase linear velocity.  The A-term is composed of processes that are velocity independent. In other words, the A-term contribution to the overall plate heigh (H) is the same regardless of linear velocity (U).  The B-term is inversely proportional to velocity.  It results from phenomena that give high plate heights at low velocities but becomes more insignificant at high velocities.  Finally, the C-term is directly proportional to linear velocity, and H increases as linear velocity increases.  Taken together, we can represent the overall plate height (H) and its dependence on mobile phase linear velocity (U) by the equation:

H = A + B/U + C*U

The relative contributions of the A-, B-, and C-terms are also shown in Figure 2.  Looking at this figure, it might now be apparent that if we can lower the contributions from one or more of the terms, we’ll end up lowering the plate height (H) at a given linear velocity.  This means the column will be more efficient and our separation will be better.  Depending on the conditions of our separation, SPPs have the possibility of improving all three of the A-, B-, and C-terms.  Let’s briefly discuss how.

A-Term

As we mentioned above, the A-term is independent of linear velocity. Generally, it can be thought of as the “multiple flow path” term that accounts for the many unequal flow paths that exist inside an HPLC column packed with spherical particles. In comparison to columns packed with similarly sized FPPs, columns packed with SPPs tend to exhibit lower A-terms. We might attribute this to two reasons. First, in the manufacturing process, SPPs are significantly more monodisperse than traditionally synthesized FPPs. In other words, there is a smaller size spread between the smallest and largest particles. Second, SPPs tend to pack more homogeneously than FPPs. This leads to flow paths that are more equivalent to one another and, ultimately, to smaller A-terms for columns packed with SPPs.

B-Term

The B-terms describes the contributions to plate height as a result of longitudinal diffusion – how much a peak spreads down the length of a column due to the analytes diffusing. Intuitively, we can understand that if we run the column at a faster velocity, there will be less time for diffusion, and the B-term contribution drops. In a real separation, we can’t eliminate all B-term diffusion, but SPPs can lower it. Note that longitudinal diffusion occurs in both the interparticle mobile phase (the space between particles) and the intraparticle mobile phase (the mobile phase inside the particle pores). Since the solid cores of SPPs reduce the intraparticle volumes, they also reduce the ability of analytes to diffuse inside the particles, thereby reducing the B-term.

C-Term

The C-term describes resistance to mass transfer, which, in essence, relates to the rate that analytes travel from the mobile phase to the stationary phase and vice versa. Due to the presence of the solid cores in SPPs, the depth to which an analyte can enter into the particle is significantly reduced. Depending on the exact experimental conditions and the nature of the analytes being separated, this effect can significantly reduce the C-term contribution to overall plate height (H).

Putting It All Together

From this discussion, we now understand how SPPs can outperform similarly-sized FPPs by improving the A-, B-, and C-term contributions to overall plate height (H). The improvements are so significant that 2.7 µm SPPs will often provide similar efficiencies as 1.8 µm FPPs, without the high cost in operating pressure. For columns of the same length, 2.7 µm SPPs can be run at about half the pressure required to run 1.8 µm FPPs at the same linear velocity.

So are there any downsides to SPPs? We already mentioned the reduced surface areas of SPPs compared to FPPs due to the presence of the solid silica cores. More often than not, however, any loss of retention that results from this can be compensated for by weakening the mobile phase a slight bit. For typical analytical separations, this is not a major concern. The greater concern arises if we consider preparative scale separations or any separation where sample loadability is a consideration. Again, due to reduced surface areas, SPPs have less stationary phase available to interact with the sample analytes. This translates to lower amounts of material that can be loaded onto a column before separation quality is impacted. Again, this isn’t a big deal for most analytical separations, but it’s something to keep in mind if we plan to scale up for preparative work.

In case you missed it, read part one of the Fast Chiral Series.

Additional Information and Resources

• Download or request a copy of our Chiral Handbook for HPLC and SFC applications here.
• Check out our chiral database with over 900 chiral applications
• Download the Chiral Stationary Phases brochure for more information about our chiral columns Chiral HPLC & SFC Columns.